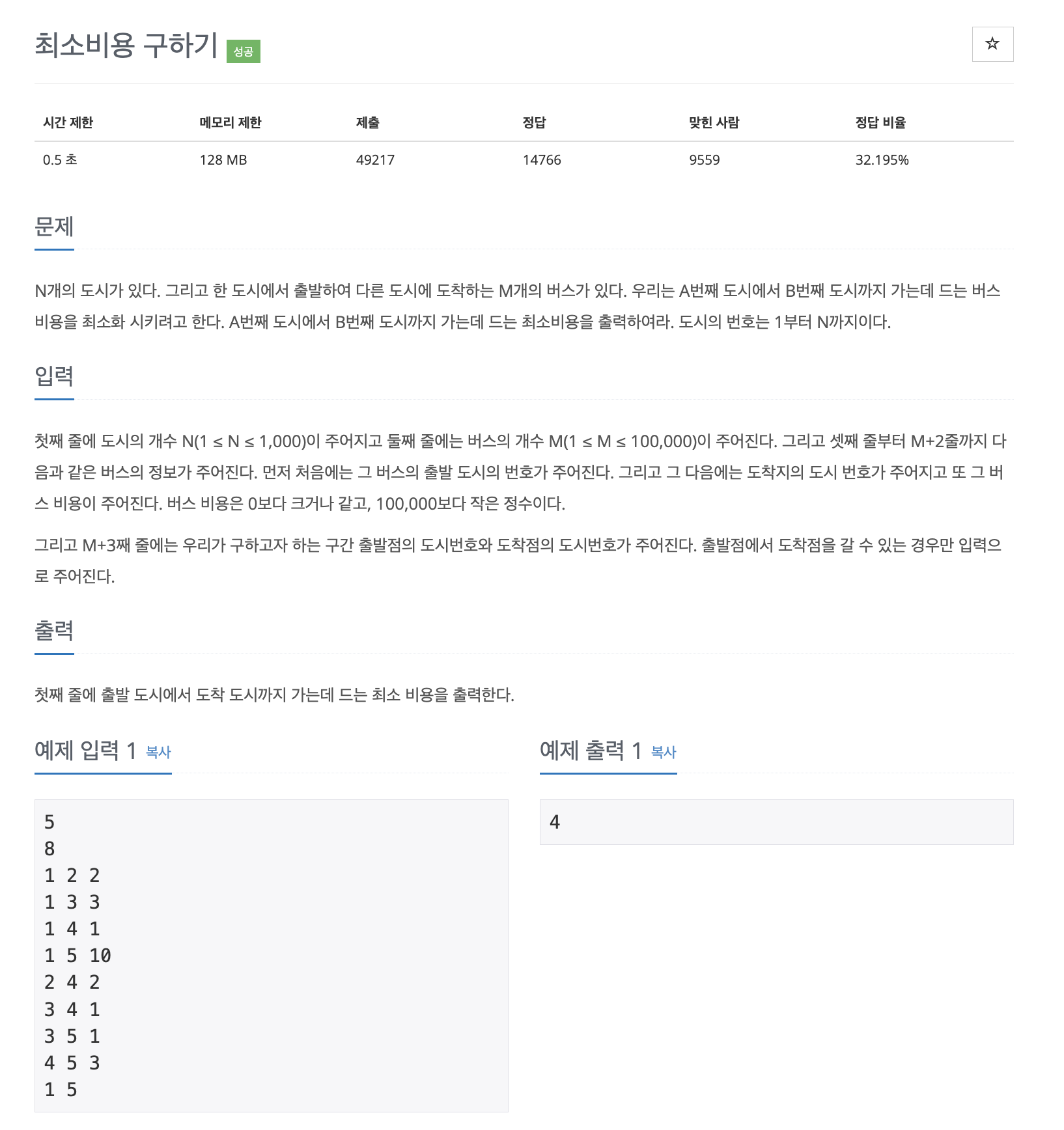
INF = 1e10
import heapq
import sys
input = sys.stdin.readline
def BOJ1916() :
N = int(input())
M = int(input())
graph = [[INF for _ in range(N+1)] for _ in range(N+1)]
for _ in range(M) :
A, B, C = map(int, input().split())
graph[A][B] = min(graph[A][B], C)
start, end = map(int, input().split())
dist = [INF for _ in range(N+1)]
# 다익스트라
def dijkstra(start) :
dist[start] = 0
heap = []
heap.append([0, start])
while heap :
curr_weight, curr_node = heapq.heappop(heap)
if dist[curr_node] < curr_weight :
continue
for idx, value in enumerate(graph[curr_node]) :
next_weight = curr_weight + value
if dist[idx] > next_weight :
dist[idx] = next_weight
heapq.heappush(heap, [next_weight, idx])
dijkstra(start)
print(dist[end])
BOJ1916()
풀이 접근 방법 :
1. 플로이드 워셜 알고리즘을 사용하면 모든 정점에서 정점간의 최소거리를 알 수 있지만 n^3으로 시간 복잡도를 가지게 된다.
해당 문제에서는 시간초과가 발생한다.
2. 다익스트라 알고리즘을 적용하였다.
다익스트라 알고리즘은 한 정점에서 모든 정점으로의 최소 거리를 구할 수 있다.
현재 노드 부터 가장 가중치가 낮은 노드부터 방문한다.(우선순위 큐 적용)
가치를 갱신할 수 있는 지점에서만 순회로 방문하면서 우선순위큐에 넣어준다
중간에 중복해서 순회하지 않도록 이미 기록되어 있는 값보다 작은 경우(값의 갱신이 필요하지 않은 경우)에는 continue를 해주었다.
https://www.acmicpc.net/problem/1916
1916번: 최소비용 구하기
첫째 줄에 도시의 개수 N(1 ≤ N ≤ 1,000)이 주어지고 둘째 줄에는 버스의 개수 M(1 ≤ M ≤ 100,000)이 주어진다. 그리고 셋째 줄부터 M+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그
www.acmicpc.net
'알고리즘' 카테고리의 다른 글
| 감소하는 수 [백준 1038] - python (0) | 2022.04.09 |
|---|---|
| 사탕 게임 [백준 3085] - python (1) | 2022.04.08 |
| 동전 2 [백준 2294] - python (0) | 2022.04.02 |
| 부분 문자열 [백준 16916] - python (0) | 2022.03.30 |
| 부분합 [백준 1806] - python (0) | 2022.03.28 |



