
import sys
input = sys.stdin.readline
def BOJ1699() :
n = int(input())
dp = [1e9 for _ in range(100001)]
dp[0] = 0
dp[1] = 1
dp[2] = 2
dp[3] = 3
for i in range(4, n+1) :
if (i ** (0.5)) % 1 == 0 :
dp[i] = 1
else :
number = int(i ** (0.5) // 1)
for j in range(1, number+1) :
if i % (j ** 2) == 0 :
dp[i] = min(dp[i], i // (j ** 2))
else :
head, _ = divmod(i, j ** 2)
dp[i] = min(dp[i], head + dp[i - head * j ** 2])
print(dp[n])
BOJ1699()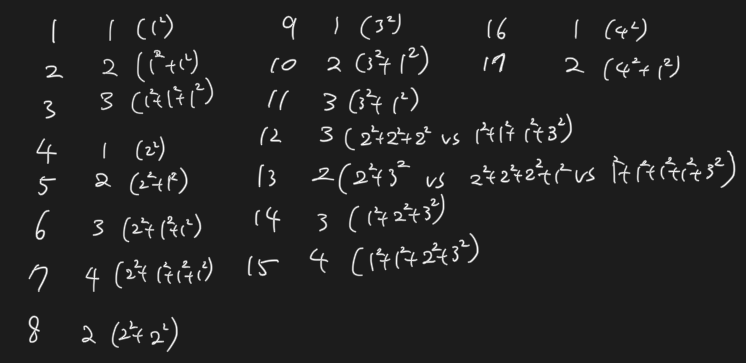
접근 방법 :
1. 구해야하는 인덱스 이전의 값들은 이미 최솟값을 구해서 가지고 있는 값들이다. 이들을 이용해야할 필요성이 다분해 보이므로 dp를 이용해 주었다.
2. 제곱수들은 최솟값 1을 가지게 된다. 직접 테스트 케이스 몇개를 그려보니 이들을 다루는 것이 핵심이 될것으로 보였다.
3. 점화식을 세워보자 n 번째 인덱스에서의 최솟값을 구하기 위해서
n번째 숫자의 제곱수 까지 (ex. 13이면 3, 17이면 4) 반복해서 탐색해 주었다.
제곱수로 나누어지게 된다면 (ex. 12와 4의 비교) 나누어진 몫이 최솟값이 될것이므로 비교를 해주었고
나누어 지지 않게 된다면 제곱수로 나눈 몫과 나머지를 이용하였다.
몫 + dp[비교 숫자 - 몫 * 제곱수] 와의 비교를 이전에 가지고 있던 값과 비교해 주었다.
dp[비교 숫자 - 몫 * 제곱수]를 이용한 이유는 이미 이전에 접근했던 배열들은 최솟값을 가지고 있기 때문에 전부 1로 채우는 것보다 최솟 값을 가질수 있을거라 판단하였다.
https://www.acmicpc.net/problem/1699
1699번: 제곱수의 합
어떤 자연수 N은 그보다 작거나 같은 제곱수들의 합으로 나타낼 수 있다. 예를 들어 11=32+12+12(3개 항)이다. 이런 표현방법은 여러 가지가 될 수 있는데, 11의 경우 11=22+22+12+12+12(5개 항)도 가능하다
www.acmicpc.net
'알고리즘' 카테고리의 다른 글
| 내리막 길[백준 1520] - python (0) | 2022.03.14 |
|---|---|
| 가장 긴 감소하는 부분 수열 [백준 11722] - python (0) | 2022.03.13 |
| 오르막 수[백준 11057] - python (0) | 2022.03.11 |
| 퇴사 [백준 14501] - python (0) | 2022.03.10 |
| 2xn 타일링 2 [백준 11727] - python (0) | 2022.03.09 |
![제곱수의 합 [백준 1699] - python](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fb30FQE%2FbtrtIkRk45G%2FPuqyioCGTaQ1UT8sio5ve0%2Fimg.png)